Decoding The Q Issue On The Smith Chart: A Deep Dive Into Resonant Circuit Evaluation

Decoding the Q Issue on the Smith Chart: A Deep Dive into Resonant Circuit Evaluation

Associated Articles: Decoding the Q Issue on the Smith Chart: A Deep Dive into Resonant Circuit Evaluation

Introduction

On this auspicious event, we’re delighted to delve into the intriguing subject associated to Decoding the Q Issue on the Smith Chart: A Deep Dive into Resonant Circuit Evaluation. Let’s weave attention-grabbing info and provide recent views to the readers.

Decoding the Q Issue on the Smith Chart: A Deep Dive into Resonant Circuit Evaluation

The Smith Chart, a ubiquitous instrument in radio frequency (RF) and microwave engineering, supplies a strong graphical illustration of impedance and reflection coefficient. Whereas primarily identified for its potential to visualise impedance matching and transmission line evaluation, it additionally provides a surprisingly insightful methodology for figuring out the standard issue (Q issue) of resonant circuits. This text delves into the intricacies of extracting Q issue info from the Smith Chart, exploring its benefits, limitations, and sensible purposes.

Understanding the Q Issue:

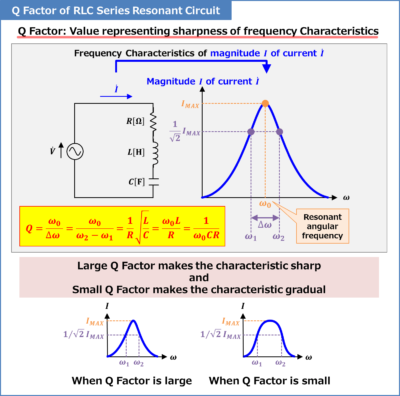
Earlier than diving into the Smith Chart illustration, let’s set up a agency understanding of the Q issue itself. The Q issue, or high quality issue, is a dimensionless parameter that describes the sharpness of resonance in a resonant system. In less complicated phrases, it quantifies how effectively a system shops vitality in comparison with the vitality it dissipates. The next Q issue signifies a sharper resonance, that means the system responds strongly solely inside a slim frequency band round its resonant frequency. Conversely, a decrease Q issue implies a broader, much less selective response.

For a collection RLC resonant circuit, the Q issue is outlined as:

Q = (ω₀L) / R = 1 / (ω₀RC)

the place:

• ω₀ is the resonant angular frequency (ω₀ = 1/√(LC))
• L is the inductance
• C is the capacitance
• R is the resistance

This equation highlights the interaction between vitality storage (L and C) and vitality dissipation (R). A excessive Q issue outcomes from a big inductance and capacitance relative to the resistance.

The Smith Chart and Impedance:

The Smith Chart’s core performance lies in its potential to map complicated impedances (Z = R + jX) onto a normalized impedance aircraft. Normalization usually includes dividing the impedance by a attribute impedance (Z₀), normally 50 ohms in lots of RF programs. This normalization permits for a compact and common illustration whatever the system’s attribute impedance. The chart’s concentric circles signify fixed resistance values (normalized), whereas the radial arcs signify fixed reactance values (normalized).

Extracting Q Issue from the Smith Chart: The Circle Methodology

The Smith Chart supplies a graphical methodology for figuring out the Q issue of a resonant circuit by analyzing the impedance locus close to resonance. This methodology depends on the truth that the impedance of a resonant circuit traces a circle on the Smith Chart because the frequency varies round resonance. This circle is sometimes called the constant-Q circle.

The steps concerned in figuring out the Q issue utilizing the Smith Chart are as follows:

1. Decide the Resonant Frequency: Establish the frequency at which the impedance is solely resistive (i.e., the imaginary half, reactance, is zero). This level lies on the horizontal axis of the Smith Chart.

2. Establish the Half-Energy Factors: The half-power factors are the frequencies at which the ability dissipated within the circuit is half the ability at resonance. These factors correspond to impedances the place the magnitude of the impedance is √2 occasions the resonant impedance. Graphically, these factors lie on the constant-Q circle on the intersections with a circle centered on the origin with a radius of √2 occasions the normalized resonant resistance.

3. Measure the Bandwidth: The bandwidth (BW) is the distinction between the 2 half-power frequencies.

4. Calculate the Q Issue: The Q issue can then be calculated utilizing the connection:

Q = f₀ / BW

the place f₀ is the resonant frequency.

Graphical Interpretation on the Smith Chart:

The constant-Q circle on the Smith Chart is centered on the horizontal axis on the normalized resonant resistance. The radius of this circle is instantly associated to the Q issue. A smaller radius signifies a decrease Q issue (broader bandwidth), whereas a bigger radius signifies the next Q issue (narrower bandwidth). This visible illustration supplies an intuitive understanding of the connection between the Q issue and the impedance variation round resonance.

Benefits of Utilizing the Smith Chart for Q Issue Willpower:

• Visible Readability: The Smith Chart supplies a transparent graphical illustration of the impedance locus and the constant-Q circle, facilitating a fast and intuitive understanding of the circuit’s habits.

• Direct Measurement: The bandwidth will be instantly measured from the Smith Chart, eliminating the necessity for complicated calculations.

• Simultaneous Impedance Matching: The Smith Chart permits for simultaneous evaluation of impedance matching and Q issue dedication, offering a complete understanding of the circuit’s efficiency.

• Appropriate for Varied Circuit Topologies: Whereas the reason targeted on collection RLC circuits, the strategy will be tailored for parallel RLC circuits and different resonant circuit configurations by appropriately remodeling the impedance.

Limitations of the Smith Chart Methodology:

• Accuracy: The accuracy of the Q issue dedication depends upon the accuracy of the Smith Chart readings and the precision of figuring out the half-power factors. For prime-Q circuits, the small bandwidth could make exact measurement difficult.

• Non-ideal Elements: The tactic assumes very best elements. Parasitic results, akin to stray capacitance and inductance, can have an effect on the accuracy of the outcomes.

• Complicated Circuits: For complicated circuits with a number of resonant frequencies, the Smith Chart methodology may turn out to be cumbersome. Software program-based simulations are sometimes most well-liked in such situations.

Functions of Smith Chart Q Issue Evaluation:

The Smith Chart methodology for figuring out the Q issue finds purposes in varied RF and microwave engineering domains:

• Filter Design: Designing filters with particular bandwidth necessities necessitates exact management over the Q issue of the resonant circuits used. The Smith Chart aids in designing and analyzing filter efficiency.

• Antenna Design: Antenna impedance matching and bandwidth are essential parameters. The Smith Chart helps in analyzing the Q issue of antenna programs and optimizing their efficiency.

• Resonant Cavity Evaluation: Understanding the Q issue of resonant cavities is significant in microwave purposes. The Smith Chart can be utilized to characterize the resonant properties of those cavities.

• Oscillator Design: The Q issue of the resonant circuit in an oscillator determines the steadiness and frequency selectivity. The Smith Chart assists in analyzing and optimizing oscillator design.

• Community Analyzer Measurements: Community analyzers usually show impedance knowledge on a Smith Chart, enabling direct Q issue dedication from measured knowledge.

Conclusion:

The Smith Chart provides a invaluable graphical instrument for figuring out the Q issue of resonant circuits. Its visible nature supplies an intuitive understanding of the connection between impedance, bandwidth, and the Q issue. Whereas limitations exist, notably relating to accuracy for high-Q circuits and complicated networks, the Smith Chart stays a strong help in RF and microwave circuit evaluation and design. Its potential to mix impedance matching evaluation with Q issue dedication makes it an indispensable instrument for engineers working in these fields. Mixed with trendy software program instruments that present correct Smith Chart representations and simulations, the strategy continues to be a cornerstone of RF and microwave engineering apply. Understanding the rules outlined on this article empowers engineers to successfully make the most of the Smith Chart for a complete evaluation of resonant circuits and their essential Q issue.

Closure

Thus, we hope this text has supplied invaluable insights into Decoding the Q Issue on the Smith Chart: A Deep Dive into Resonant Circuit Evaluation. We thanks for taking the time to learn this text. See you in our subsequent article!