Decoding the t-Distribution Desk: A Complete Information
Associated Articles: Decoding the t-Distribution Desk: A Complete Information
Introduction
With nice pleasure, we’ll discover the intriguing subject associated to Decoding the t-Distribution Desk: A Complete Information. Let’s weave attention-grabbing data and supply recent views to the readers.
Desk of Content material
Decoding the t-Distribution Desk: A Complete Information

The t-distribution, a cornerstone of inferential statistics, is essential for speculation testing and confidence interval development when coping with small pattern sizes or unknown inhabitants normal deviations. In contrast to the traditional distribution, the t-distribution is a household of curves, every outlined by its levels of freedom (df). Understanding the best way to use a t-distribution desk is crucial for appropriately decoding statistical outcomes. This text offers a complete information to navigating and decoding t-distribution tables, masking their construction, software, and customary pitfalls.
Understanding the t-Distribution
The t-distribution, also called Pupil’s t-distribution, is comparable in form to the usual regular distribution (Z-distribution), exhibiting a bell-shaped curve symmetrical round a imply of zero. Nonetheless, it possesses heavier tails, that means it has a better likelihood of observing excessive values. This attribute stems from the truth that the t-distribution accounts for the uncertainty launched by estimating the inhabitants normal deviation from a pattern. Because the pattern measurement will increase, the t-distribution progressively approaches the traditional distribution.
The important thing parameter defining a selected t-distribution is its levels of freedom (df). The levels of freedom signify the variety of impartial items of knowledge out there to estimate a parameter. In easy phrases, for a single pattern t-test, the levels of freedom are calculated as:
df = n – 1
the place ‘n’ is the pattern measurement. Thus, a pattern of 10 observations would have 9 levels of freedom (df = 10 – 1 = 9). Totally different levels of freedom result in completely different t-distributions, with decrease levels of freedom leading to wider, flatter curves and better levels of freedom leading to curves nearer to the traditional distribution.
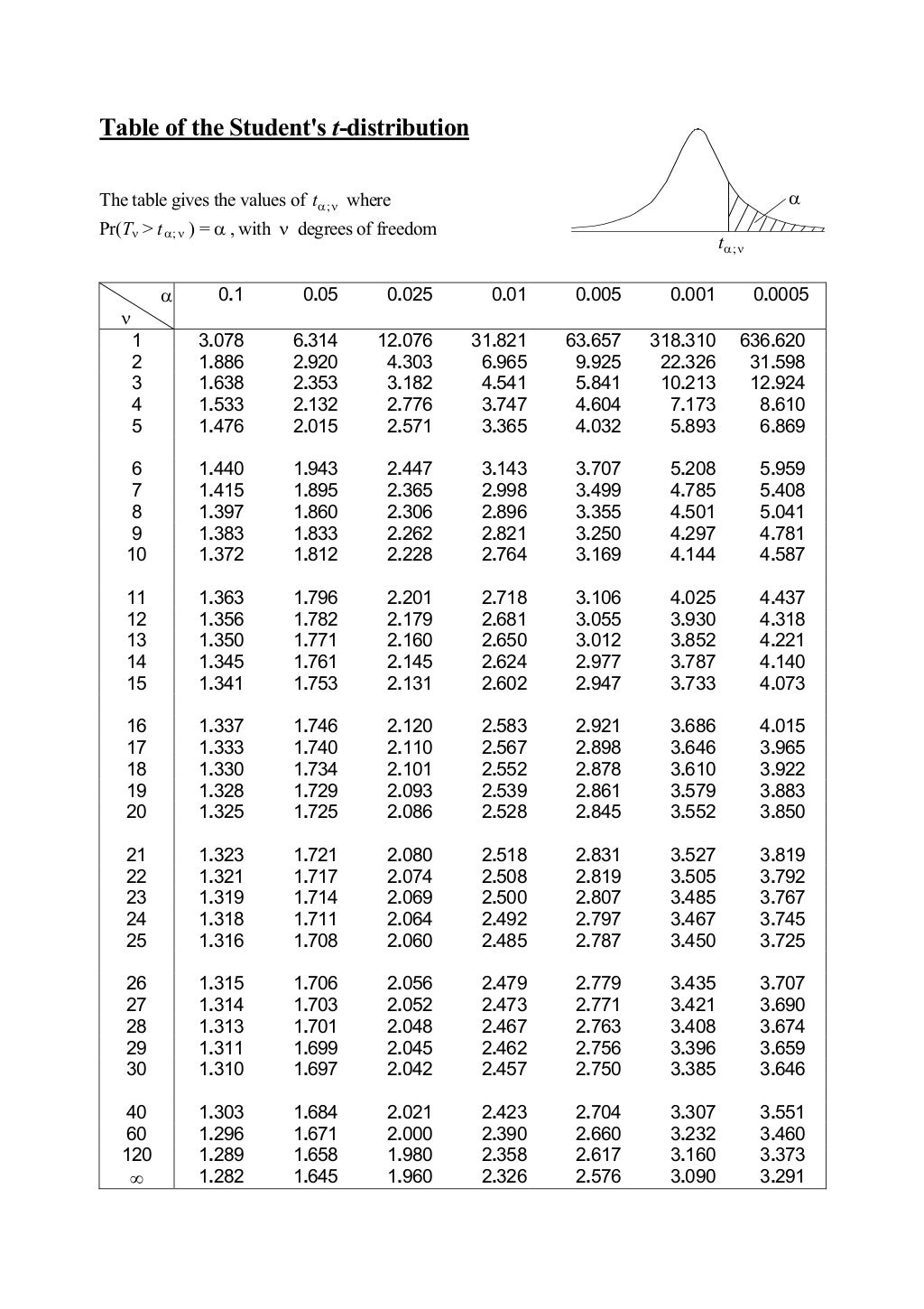
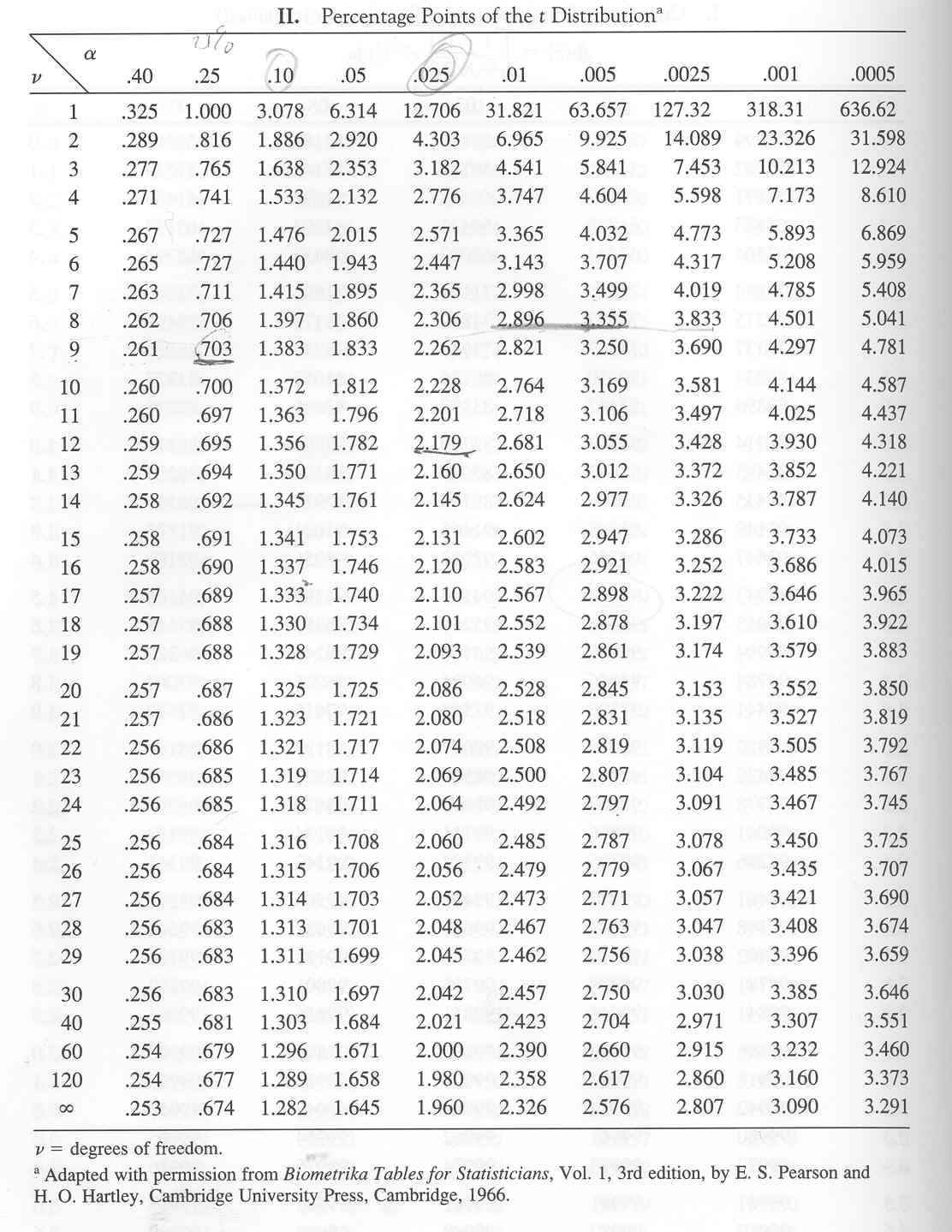
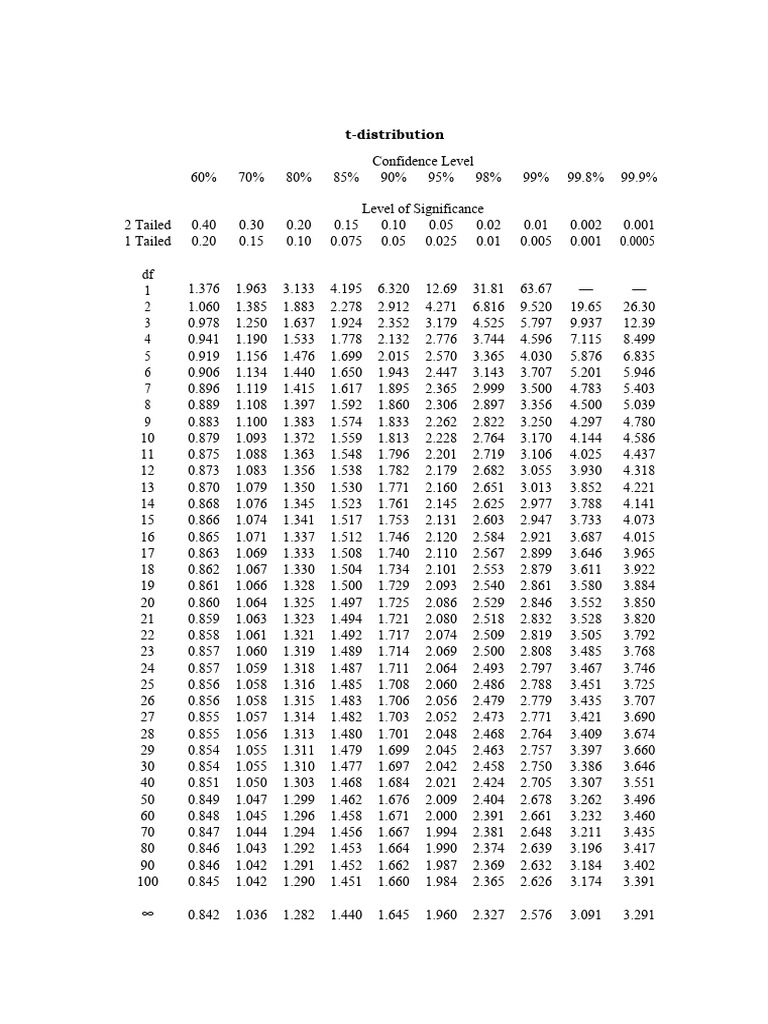
Construction of a t-Distribution Desk
A typical t-distribution desk is organized in a grid format. The rows signify the levels of freedom (df), usually starting from 1 to infinity (usually represented by a big worth like 100 or 1000, which approximates the traditional distribution). The columns signify the likelihood (p) or alpha (α) degree, which corresponds to the world within the tail(s) of the t-distribution. These chances are often given as one-tailed (representing the likelihood in a single tail) or two-tailed (representing the likelihood in each tails mixed).
Deciphering the Desk Entries
The entries inside the desk signify the vital t-values. These are the t-scores that correspond to a selected likelihood degree and levels of freedom. For instance, in the event you discover the intersection of df = 10 and a two-tailed likelihood of 0.05 (α = 0.05), the desk entry would be the t-value such that 5% of the world beneath the t-distribution curve with 10 levels of freedom lies within the two tails mixed. This t-value is used as a threshold in speculation testing.
Utilizing the t-Distribution Desk for Speculation Testing
The t-distribution desk is instrumental in conducting t-tests, that are used to match means. The method usually includes these steps:
- State the hypotheses: Formulate the null and different hypotheses.
- Decide the importance degree (α): That is the likelihood of rejecting the null speculation when it’s really true (Sort I error). Widespread values are 0.05 and 0.01.
- Calculate the t-statistic: This can be a measure of the distinction between the pattern imply and the hypothesized inhabitants imply, standardized by the pattern normal error. The method varies relying on the kind of t-test (one-sample, two-sample impartial, paired samples).
- Decide the levels of freedom (df): This relies on the precise t-test used.
- Discover the vital t-value: Find the vital t-value within the t-distribution desk comparable to the chosen significance degree (α) and the calculated levels of freedom (df). Bear in mind to make use of a one-tailed or two-tailed vital worth relying on the choice speculation.
- Examine the calculated t-statistic to the vital t-value: If absolutely the worth of the calculated t-statistic is bigger than the vital t-value, the null speculation is rejected. In any other case, the null speculation will not be rejected.
One-tailed vs. Two-tailed Exams
The selection between a one-tailed and a two-tailed take a look at relies on the analysis query.
- One-tailed take a look at: Used when you might have a directional speculation (e.g., "the imply is bigger than X" or "the imply is lower than X"). The whole significance degree (α) is positioned in a single tail of the distribution.
- Two-tailed take a look at: Used when you might have a non-directional speculation (e.g., "the imply is completely different from X"). The importance degree (α) is split equally between the 2 tails of the distribution.
Confidence Intervals and the t-Distribution
The t-distribution can be used to assemble confidence intervals, which give a variety of believable values for a inhabitants parameter. The method for a confidence interval for a inhabitants imply is:
*Pattern imply ± (t-critical worth) (Customary error)**
The t-critical worth is obtained from the t-distribution desk, utilizing the specified confidence degree (e.g., 95% confidence corresponds to α = 0.05) and the levels of freedom.
Limitations of the t-Distribution Desk
Whereas t-distribution tables are broadly used, they’ve some limitations:
- Restricted precision: Tables usually present t-values to just a few decimal locations, probably resulting in slight inaccuracies. Statistical software program offers extra exact values.
- Interpolation required: If the precise levels of freedom aren’t out there within the desk, interpolation could also be crucial, introducing additional potential error.
- Assumption of normality: The t-test assumes that the underlying information is roughly usually distributed. If this assumption is severely violated, the outcomes of the t-test could also be unreliable.
Alternate options to t-Distribution Tables
With the appearance of statistical software program packages (like R, SPSS, SAS, Python with SciPy), the necessity for guide lookup in t-distribution tables has diminished considerably. These software program packages present exact t-values and automate the complete speculation testing course of, eliminating the necessity for guide calculations and desk lookups. In addition they supply varied non-parametric checks as options when the idea of normality is violated.
Conclusion
The t-distribution desk is a helpful device for understanding and making use of the t-distribution in statistical evaluation. Whereas its use is reducing because of the availability of statistical software program, understanding its construction and interpretation stays essential for comprehending the basic rules of speculation testing and confidence interval development. By mastering the usage of the t-distribution desk and understanding its limitations, researchers can successfully analyze information and draw legitimate conclusions, even with small pattern sizes. Nonetheless, it is important to do not forget that statistical software program offers a extra correct and environment friendly method for conducting t-tests and setting up confidence intervals, minimizing potential errors related to guide calculations and desk interpolation.




Closure
Thus, we hope this text has supplied helpful insights into Decoding the t-Distribution Desk: A Complete Information. We hope you discover this text informative and useful. See you in our subsequent article!
